calculus algebraic numerical graphical pdf

Calculus combines algebraic, numerical, and graphical approaches to analyze change and accumulation, offering a comprehensive framework for problem-solving in mathematics and real-world applications.

Overview of the Three Core Methods

The three core methods in calculus—algebraic, numerical, and graphical—each offer distinct approaches to understanding mathematical problems. The algebraic method relies on symbolic manipulation and exact solutions, providing a rigorous foundation. Numerical methods, such as Riemann sums and Euler’s method, enable approximations for complex problems where exact solutions may be elusive. Graphical methods visualize functions and their properties, aiding in conceptual understanding. Together, these approaches provide a comprehensive toolkit for analyzing change and accumulation, allowing for a deeper and more versatile grasp of calculus concepts.

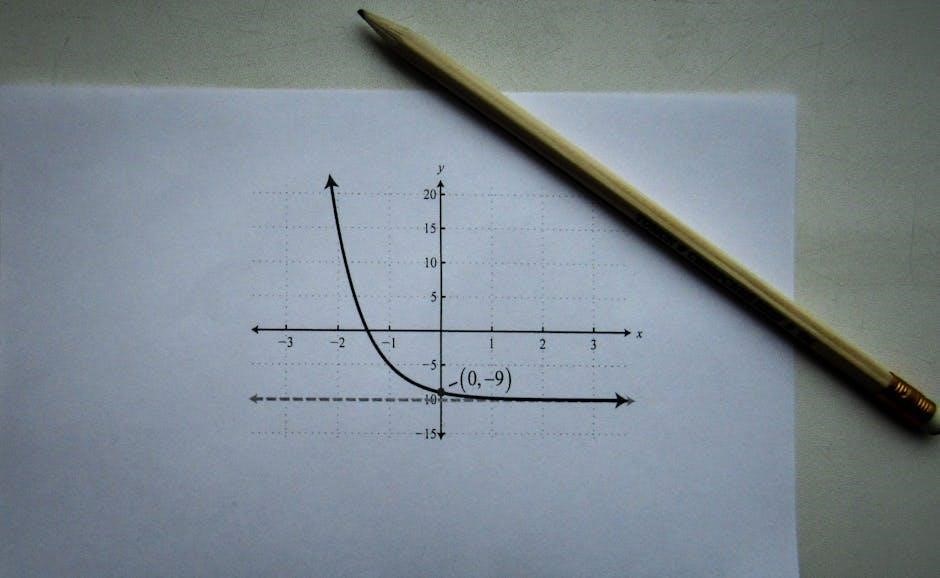
The Importance of Integration in Problem-Solving

Integration is a cornerstone of calculus, enabling the calculation of areas under curves, volumes of solids, and accumulation over intervals; It provides precise methods for solving problems involving continuous change, such as distance traveled or work done. Algebraic integration offers exact solutions through antiderivatives, while numerical integration approximates complex integrals. Graphical interpretations visualize the accumulation process, deepening understanding. Together, these approaches make integration an indispensable tool for modeling real-world phenomena in physics, engineering, and economics. Mastery of integration enhances problem-solving skills across diverse applications, bridging theory and practical implementation.

Algebraic Methods in Calculus

Algebraic methods in calculus rely on symbolic manipulation and exact solutions, providing precise results through formulas and equations, which are fundamental to the discipline.

Symbolic Manipulation and Exact Solutions

Symbolic manipulation is a cornerstone of algebraic methods in calculus, enabling exact solutions through precise mathematical formulations. By leveraging algebraic techniques, students can solve equations, simplify expressions, and derive functions analytically. This approach avoids approximations, delivering unambiguous results essential for understanding fundamental concepts. Exact solutions are particularly vital in optimization problems, differential equations, and limit evaluations. Techniques like factoring, polynomial division, and trigonometric identities are indispensable tools. These methods not only provide clarity but also form the foundation for advanced calculus topics, ensuring a robust mathematical framework for problem-solving.

Formulas and Equations: The Foundation of Calculus

Formulas and equations are the bedrock of calculus, providing the mathematical language to describe and analyze change and accumulation. From basic derivative rules to integral formulas, these expressions enable precise problem-solving. Algebraic methods rely on these tools to derive exact solutions, while numerical and graphical approaches often reference them for validation. Mastering key equations, such as the Fundamental Theorem of Calculus, is essential for understanding the subject’s core principles. These formulas also bridge calculus to real-world applications in physics, engineering, and economics, making them indispensable for both theoretical and practical problem-solving.

Numerical Methods in Calculus

Numerical methods provide approximate solutions for complex calculus problems, using techniques like Riemann sums and Euler’s method to estimate integrals and solve differential equations effectively.

Approximation Techniques: Riemann Sums and Newton’s Method

Riemann sums and Newton’s method are cornerstone numerical techniques in calculus. Riemann sums approximate definite integrals by dividing the area under a curve into shapes like rectangles or trapezoids, providing an estimate of the total area. This method is foundational for understanding integration and is widely used in real-world applications. Newton’s method, on the other hand, is an iterative approach to finding roots of equations, offering an efficient way to approximate solutions when exact algebraic methods are complex or unavailable. Together, these techniques bridge the gap between theoretical calculus and practical problem-solving, enabling accurate and efficient approximations.

Euler’s Method for Solving Differential Equations

Euler’s method is a numerical technique for approximating solutions to ordinary differential equations (ODEs) when exact algebraic solutions are difficult to obtain. It uses an iterative approach, starting with an initial value and estimating subsequent values by stepping through the domain. The method relies on the derivative at each point to calculate the next value, making it straightforward to implement. While it is less accurate over large intervals due to error accumulation, Euler’s method is a valuable tool for introducing numerical solutions and understanding the behavior of ODEs graphically. It is often used in educational settings to bridge algebraic and graphical approaches in calculus.

Graphical Methods in Calculus

Graphical methods in calculus involve visualizing functions and their properties to understand concepts like limits, continuity, and derivatives through graphs and tables.

Visualizing Functions and Their Properties

Visualizing functions and their properties is essential for understanding calculus concepts. By analyzing graphs, students can identify key features such as intercepts, asymptotes, and turning points. Graphical representations help illustrate behavior like increasing/decreasing intervals, concavity, and points of inflection. Tools like graphing calculators and software enable detailed exploration, allowing learners to connect algebraic expressions with their visual counterparts. This method enhances comprehension of complex relationships and supports problem-solving in calculus.

Using Graphs to Understand Limits and Continuity

Graphs are invaluable for understanding limits and continuity in calculus. By analyzing function behavior visually, students can identify discontinuities, such as removable holes or jumps. Graphical tools allow exploration of one-sided limits and infinite limits, aiding in conceptual understanding. Visual representations also clarify the relationship between function behavior and limit properties, reinforcing algebraic and numerical methods. This approach aligns with the Rule of Four, emphasizing the integration of graphical, algebraic, numerical, and verbal representations for a deeper grasp of calculus fundamentals.

Interplay Between Algebraic, Numerical, and Graphical Methods

Algebraic, numerical, and graphical methods complement each other, offering unique strengths and insights. Together, they provide a holistic understanding of calculus concepts and problem-solving strategies.

The Rule of Four: Combining Representations for Deeper Understanding

The Rule of Four emphasizes the integration of algebraic, numerical, graphical, and verbal methods to represent and solve calculus problems. This approach fosters a comprehensive understanding by leveraging the strengths of each method. Algebraic techniques provide exact solutions, while numerical methods offer approximations. Graphical representations visualize relationships, and verbal descriptions contextualize concepts. Together, these methods enhance problem-solving skills and deepen insights into calculus principles. Educational resources like Calculus: Graphical, Numerical, Algebraic by Ross L. Finney align with this framework, offering students and teachers structured support to master these interconnected approaches. This holistic learning strategy prepares learners for real-world applications and advanced mathematical studies.

Real-World Applications of Integrated Approaches

Integrated calculus approaches are essential in real-world problem-solving, combining algebraic precision, numerical approximations, and graphical insights. Engineers use these methods to optimize designs, model population growth, and analyze fluid dynamics. In economics, they predict market trends and evaluate financial models. Medical imaging relies on graphical and numerical techniques to process data. These approaches also aid in understanding climate patterns and resource allocation. By merging algebraic, numerical, and graphical tools, professionals tackle complex challenges effectively. Educational resources like Finney’s Calculus: Graphical, Numerical, Algebraic prepare students for these practical applications, emphasizing the value of integrated learning in diverse fields.

Educational Resources and PDF Materials

Access Calculus: Graphical, Numerical, Algebraic by Ross L. Finney in PDF for comprehensive learning. Online guides and worksheets offer practice problems, enhancing understanding and skill development.

Calculus: Graphical, Numerical, Algebraic (5th Edition) by Ross L. Finney

Calculus: Graphical, Numerical, Algebraic (5th Edition) by Ross L. Finney is a comprehensive textbook designed for high school and college students. It aligns with the AP Calculus syllabus, emphasizing the Rule of Four: algebraic, numerical, graphical, and verbal methods. The book provides enhanced student and teacher support, including updated examples, exercises, and real-world applications. It integrates modern tools and technologies, making calculus accessible and engaging. This edition focuses on developing a deeper understanding of calculus through multiple representations, fostering analytical and problem-solving skills. It is available in PDF format for easy access and study.

Online PDF Guides and Worksheets for Practice

Online PDF guides and worksheets are invaluable resources for mastering calculus concepts. These materials provide structured exercises, examples, and solutions covering algebraic, numerical, and graphical methods. Many resources focus on specific topics like Riemann sums, differential equations, and limit analysis. Worksheets often align with AP Calculus syllabus changes, ensuring relevance to modern exam formats. Additionally, interactive PDF guides offer visual aids and step-by-step explanations, enhancing understanding. Platforms like Jupyter Notebooks and Sage further support numerical and graphical explorations. These tools are accessible online, making practice convenient and comprehensive for learners at all levels.

Future Directions in Calculus Education

Advancements in interactive tools like Jupyter Notebooks and Sage are revolutionizing calculus education, enhancing problem-solving and visualization. Modern technologies are making learning more dynamic and accessible.

Modern Tools and Technologies in Teaching Calculus

Modern tools like Jupyter Notebooks and Sage are transforming calculus education by enabling interactive computations and visualizations. These technologies allow students to explore complex concepts through dynamic simulations and real-time problem-solving. Interactive platforms provide a hands-on learning experience, making abstract ideas more tangible. Additionally, digital textbooks and PDF resources, such as the 5th edition of Calculus: Graphical, Numerical, Algebraic, are being enhanced with multimedia elements to support diverse learning styles. These advancements align with the evolving AP Calculus syllabus, ensuring students are well-prepared for modern mathematical challenges.

Aligning with AP Calculus Syllabus and Exam Changes

The 5th edition of Calculus: Graphical, Numerical, Algebraic by Ross L. Finney is specifically aligned with the updated AP Calculus syllabus, ensuring comprehensive coverage of required topics. This edition includes enhanced student and teacher support, featuring updated examples and exercises that reflect current AP exam questions. By integrating algebraic, numerical, and graphical methods, the text provides a unified approach to understanding calculus concepts. These resources are designed to help students and educators meet the challenges of the evolving AP curriculum, fostering deeper mathematical understanding and problem-solving skills.